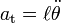Ecuaciones
Todos los cálculos relacionados con las magnitudes que describen los movimientos rectilíneos podemos hacerlos con estas dos ecuaciones:
| e = eo + vo·t + ½·a·t² |
| vf = vo + a·t |
e es el desplazamiento del móvil
eo es la posición inicial
t es el intervalo de tiempo que estamos considerando
vo es la velocidad inicial (al principio de nuestro intervalo de tiempo)
vf es la velocidad final (al final de nuestro intervalo de tiempo)
a es la aceleración
Estas ecuaciones se pueden adaptar según las características concretas del movimiento que estemos estudiando:
Si el móvil parte del orígen de coordenadas
Significa que la posición inicial eo del cuerpo es cero. En este caso la ecuación del desplazamiento podemos escribirla así:
Si el móvil parte del reposo
Esto quiere decir que la velocidad inicial es cero. Al sustituir este valor en las ecuaciones anteriores, queda:
Si el movimiento es uniforme
Es el movimiento de velocidad constante, es decir el movimiento con aceleración cero.
Al dar valor 0 a la aceleración, las ecuaciones del principio quedan así:
Ya habrás notado que no se trata de ecuaciones diferentes sino de las mismas ecuaciones adaptadas a dos casos concretos, por tanto no es necesario que aprendas de memoria todas las ecuaciones: con las dos primeras y un análisis de la situación tienes suficiente.
Cómo resolver los ejercicios
Para resolver un ejercicio no basta con aplicar las ecuaciones. Es necesario seguir un método o estrategia que podemos resumir así:
- Dibuja un diagrama con la situación propuesta.
- Identifica las variables que conocemos y ponlas en una lista de datos.
- Identifica las variables desconocidas y ponlas en la lista de incógnitas.
- Identifica la ecuación con la que vas a obtener el resultado y comprueba si tienes todos los datos necesarios o debes calcular alguno con la otra ecuación.
- Sustituye los valores en las ecuaciones y realiza los pasos y las operaciones que necesites para obtener el resultado.
- Comprueba que tu resultado sea correcto matemáticamente y que sea razonable desde el punto de vista físico.
Ejemplo
|
Imagina que el conductor de una moto que circula 25 m/s pisa el freno hasta detenerse cuando ve que el semáforo se pone en ámbar. Si los frenos producen una aceleración de -5 m/s², ¿cuál será el desplazamiento durante el proceso de frenado?
|
Comenzamos haciendo un esquema informativo de la situación física, que aparece un poco más abajo.
El segundo paso consiste en identificar los datos que nos proporcionan. Observa que la velocidad final vf es cero porque nos dicen que la moto se detiene. La velocidad inicial vo de la moto es +25 m/s porque esa es la velocidad al inicio del movimiento que estamos estudiando (el movimiento de frenado). La aceleración a es -5 m/s². Presta mucha atención a los signos + y - que tienen las magnitudes.
El siguiente paso es saber qué queremos calcular. En nuestro caso, tenemos que determinar el desplazamiento e de la moto mientras frena.
A continuación tienes el resultado de los tres primeros pasos:
Esquema:
|
Datos:
vo = +25 m/s
vf = 0 m/s
a = -5 m/s²
|
Buscamos:
e = ?
|
El cuarto paso consiste en decidir con qué ecuación podemos calcular lo que nos piden y comprobar si tenemos todos los datos que necesitamos. En nuestro caso usaremos la ecuación:
Observa que no podemos calcular e hasta que conozcamos el tiempo t que dura la frenada. Lo podemos calcular con la otra ecuación:
Si sustituimos los valores conocidos de vf, vo y a, tenemos:
0 = 25 m/s + (-5) m/s²·t
-25 m/s = -5 m/s²·t
t = -25 m/s / -5 m/s² = 5 s
Una vez calculado el tiempo que dura el movimiento, procedemos a determinar el desplazamiento:
e = 25 m/s · 5s + ½ (-5)m/s²·(5s)²
e = 125 m - 62,5 m = 62,5 m
e = 62,5 m
Hemos llegado a la conclusión de que la moto recorre 62,5 m durante el proceso de frenada.
El último paso consiste en comprobar que la solución que damos es correcta y razonable. La solución, en este caso, representa el desplazamiento que realiza la moto desde que se pisa el freno hasta que se detiene. Parece razonable que si se circula a 90 km/h (25 m/s), la distancia necesaria para detener la moto sea aproximadamente las dos terceras partes de un campo de fútbol, similar a la que nosotros hemos obtenido.
Para comprobar si los cálculos matemáticos son correctos, sustituye los valores de t y de e que hemos calculado en ambas ecuaciones del movimiento y comprueba que la parte izquierda de cada ecuación sea igual que la derecha.
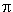 )° = 57.296°
)° = 57.296°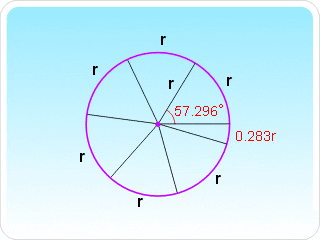
 , que subtiende una circunferencia de radio r, medido en radianes, es:
, que subtiende una circunferencia de radio r, medido en radianes, es: , que subtiende una circunferencia de radio r, medido en radianes, es:
, que subtiende una circunferencia de radio r, medido en radianes, es:
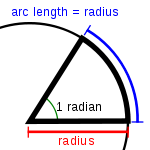


 es la amplitud de una onda (la elongación máxima o altura de la cresta de la onda). Las unidades de amplitud dependen del tipo de onda — las ondas en una cuerda tienen una amplitud expresada como una distancia (metros), las ondas sonoras como presión (pascales) y ondas electromagnéticas como la amplitud del campo eléctrico (voltios/metros). La amplitud puede ser constante, o puede variar con el tiempo y/o posición. La forma de la variación de amplitud es llamada la envolvente de la onda.
es la amplitud de una onda (la elongación máxima o altura de la cresta de la onda). Las unidades de amplitud dependen del tipo de onda — las ondas en una cuerda tienen una amplitud expresada como una distancia (metros), las ondas sonoras como presión (pascales) y ondas electromagnéticas como la amplitud del campo eléctrico (voltios/metros). La amplitud puede ser constante, o puede variar con el tiempo y/o posición. La forma de la variación de amplitud es llamada la envolvente de la onda. ) es la distancia entre dos crestas o valles seguidos. Se mide en unidades de longitud, tales como el metro(m), sus múltiplo o submúltipos según convenga. Así, en la óptica, la longitud de onda de la luz se mide en nanómetros.
) es la distancia entre dos crestas o valles seguidos. Se mide en unidades de longitud, tales como el metro(m), sus múltiplo o submúltipos según convenga. Así, en la óptica, la longitud de onda de la luz se mide en nanómetros. puede ser asociado con la longitud de onda por la relación:
puede ser asociado con la longitud de onda por la relación:
 El periodo
El periodo  es el tiempo requerido para que el movimiento de oscilación de la onda describa un ciclo completo. La frecuencia
es el tiempo requerido para que el movimiento de oscilación de la onda describa un ciclo completo. La frecuencia  es el número de ciclos completos transcurridos en la unidad de tiempo (por ejemplo, un segundo). Es medida en hercios. Matemáticamente se define sin ambigüedad como:
es el número de ciclos completos transcurridos en la unidad de tiempo (por ejemplo, un segundo). Es medida en hercios. Matemáticamente se define sin ambigüedad como: representa la frecuencia en radianes por segundo. Está relacionada con la frecuencia por
representa la frecuencia en radianes por segundo. Está relacionada con la frecuencia por


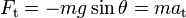
 tiene dirección opuesta a la del desplazamiento angular positivo (hacia la derecha, en la figura). Considerando la relación existente entre la aceleración tangencial y la aceleración angular
tiene dirección opuesta a la del desplazamiento angular positivo (hacia la derecha, en la figura). Considerando la relación existente entre la aceleración tangencial y la aceleración angular